OPEN-SOURCE SCRIPT
Executive Stock Options [Loxx]
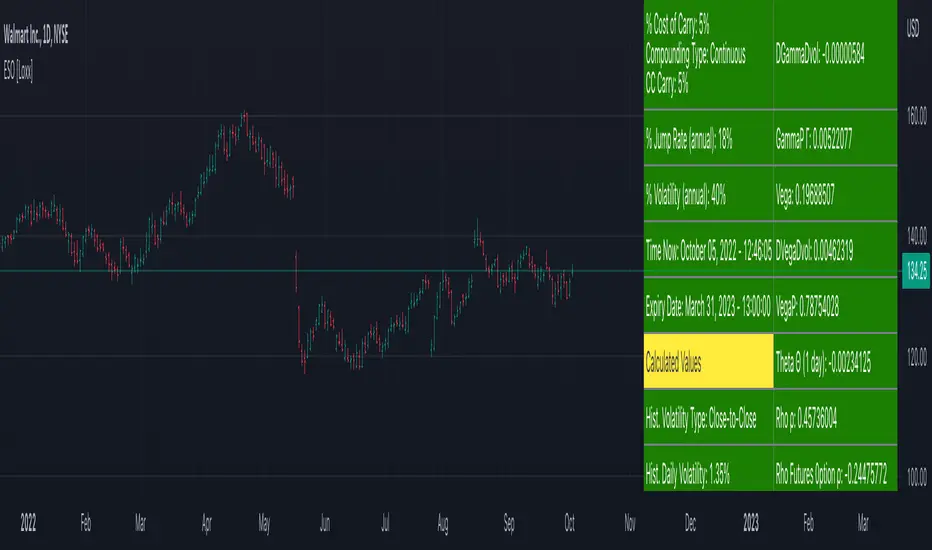
The Jennergren and Naslund (1993) formula takes into account that an employee or executive often loses her options if she has to leave the company before the option's expiration: (via "The Complete Guide to Option Pricing Formulas")
c = e^(-lambda*T) * (Se^((b-r)T) * N(d1) - Xe^-rT * N(d2))
p = e^(-lambda*T) * (Xe^(-rT) * N(-d2) - Se^(b-r)T * N(-d1))
where
d1 = (log(S/X) + (b + v^2/2)T) / vT^0.5
d2 = d1 - vT^0.5
lambda is the jump rate per year. The value of the executive option equals the ordinary Black-Scholes option price multiplied by the probability e —AT that the executive will stay with the firm until the option expires.
b=r options on non-dividend paying stock
b=r-q options on stock or index paying a dividend yield of q
b=0 options on futures
b=r-rf currency options (where rf is the rate in the second currency)
Inputs
S = Stock price.
K = Strike price of option.
T = Time to expiration in years.
r = Risk-free rate
c = Cost of Carry
V = Variance of the underlying asset price
lambda = Jump rate per year
cnd1(x) = Cumulative Normal Distribution
nd(x) = Standard Normal Density Function
convertingToCCRate(r, cmp ) = Rate compounder
Numerical Greeks or Greeks by Finite Difference
Analytical Greeks are the standard approach to estimating Delta, Gamma etc... That is what we typically use when we can derive from closed form solutions. Normally, these are well-defined and available in text books. Previously, we relied on closed form solutions for the call or put formulae differentiated with respect to the Black Scholes parameters. When Greeks formulae are difficult to develop or tease out, we can alternatively employ numerical Greeks - sometimes referred to finite difference approximations. A key advantage of numerical Greeks relates to their estimation independent of deriving mathematical Greeks. This could be important when we examine American options where there may not technically exist an exact closed form solution that is straightforward to work with. (via VinegarHill FinanceLabs)
Things to know
Only works on the daily timeframe and for the current source price.
You can adjust the text size to fit the screen
c = e^(-lambda*T) * (Se^((b-r)T) * N(d1) - Xe^-rT * N(d2))
p = e^(-lambda*T) * (Xe^(-rT) * N(-d2) - Se^(b-r)T * N(-d1))
where
d1 = (log(S/X) + (b + v^2/2)T) / vT^0.5
d2 = d1 - vT^0.5
lambda is the jump rate per year. The value of the executive option equals the ordinary Black-Scholes option price multiplied by the probability e —AT that the executive will stay with the firm until the option expires.
b=r options on non-dividend paying stock
b=r-q options on stock or index paying a dividend yield of q
b=0 options on futures
b=r-rf currency options (where rf is the rate in the second currency)
Inputs
S = Stock price.
K = Strike price of option.
T = Time to expiration in years.
r = Risk-free rate
c = Cost of Carry
V = Variance of the underlying asset price
lambda = Jump rate per year
cnd1(x) = Cumulative Normal Distribution
nd(x) = Standard Normal Density Function
convertingToCCRate(r, cmp ) = Rate compounder
Numerical Greeks or Greeks by Finite Difference
Analytical Greeks are the standard approach to estimating Delta, Gamma etc... That is what we typically use when we can derive from closed form solutions. Normally, these are well-defined and available in text books. Previously, we relied on closed form solutions for the call or put formulae differentiated with respect to the Black Scholes parameters. When Greeks formulae are difficult to develop or tease out, we can alternatively employ numerical Greeks - sometimes referred to finite difference approximations. A key advantage of numerical Greeks relates to their estimation independent of deriving mathematical Greeks. This could be important when we examine American options where there may not technically exist an exact closed form solution that is straightforward to work with. (via VinegarHill FinanceLabs)
Things to know
Only works on the daily timeframe and for the current source price.
You can adjust the text size to fit the screen
Versionshinweise
Corrected static time.Versionshinweise
Corrected UI error. Also, v is volatility not variance in the description above. Open-source Skript
Ganz im Sinne von TradingView hat dieser Autor sein/ihr Script als Open-Source veröffentlicht. Auf diese Weise können nun das Script auch andere Trader verstehen und prüfen. Vielen Dank an den Autor! Sie können das Script kostenlos verwenden. Die Nutzung dieses Codes in einer Veröffentlichung wird in unseren Hausregeln reguliert. Sie können es als Favoriten auswählen, um es in einem Chart zu verwenden.
Möchten Sie dieses Skript auf einem Chart verwenden?
Public Telegram Group, t.me/algxtrading_public
VIP Membership Info: patreon.com/algxtrading/membership
VIP Membership Info: patreon.com/algxtrading/membership
Haftungsausschluss
Die Informationen und Veröffentlichungen sind nicht als Finanz-, Anlage-, Handels- oder andere Arten von Ratschlägen oder Empfehlungen gedacht, die von TradingView bereitgestellt oder gebilligt werden, und stellen diese nicht dar. Lesen Sie mehr in den Nutzungsbedingungen.